Machine learning has demonstrated dramatic effectiveness in a wide range of fields, including computer security. However, machine learning for computer security has its weaknesses. This does not mean that machine learning is not useful; rather, it means that machine learning itself has an attack surface that must be minimized.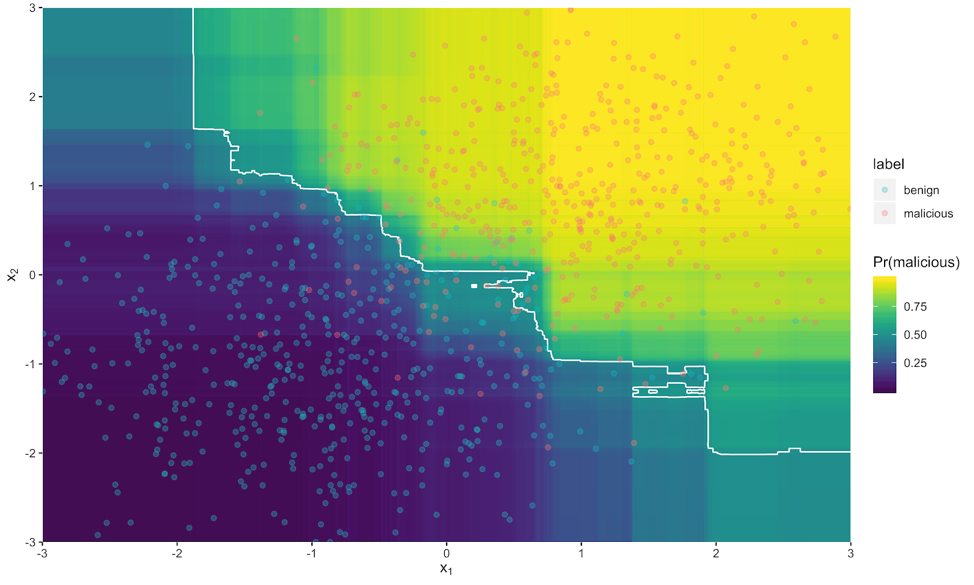 Figure 1 is a toy example of the classification boundary of a machine learning model using two input features x1, x2 . Some of the malicious examples fall on the wrong side of the boundary, so they are evasive. Additionally, some of the benign examples are false-positives because they are misclassified as malicious.
Figure 1 is a toy example of the classification boundary of a machine learning model using two input features x1, x2 . Some of the malicious examples fall on the wrong side of the boundary, so they are evasive. Additionally, some of the benign examples are false-positives because they are misclassified as malicious.
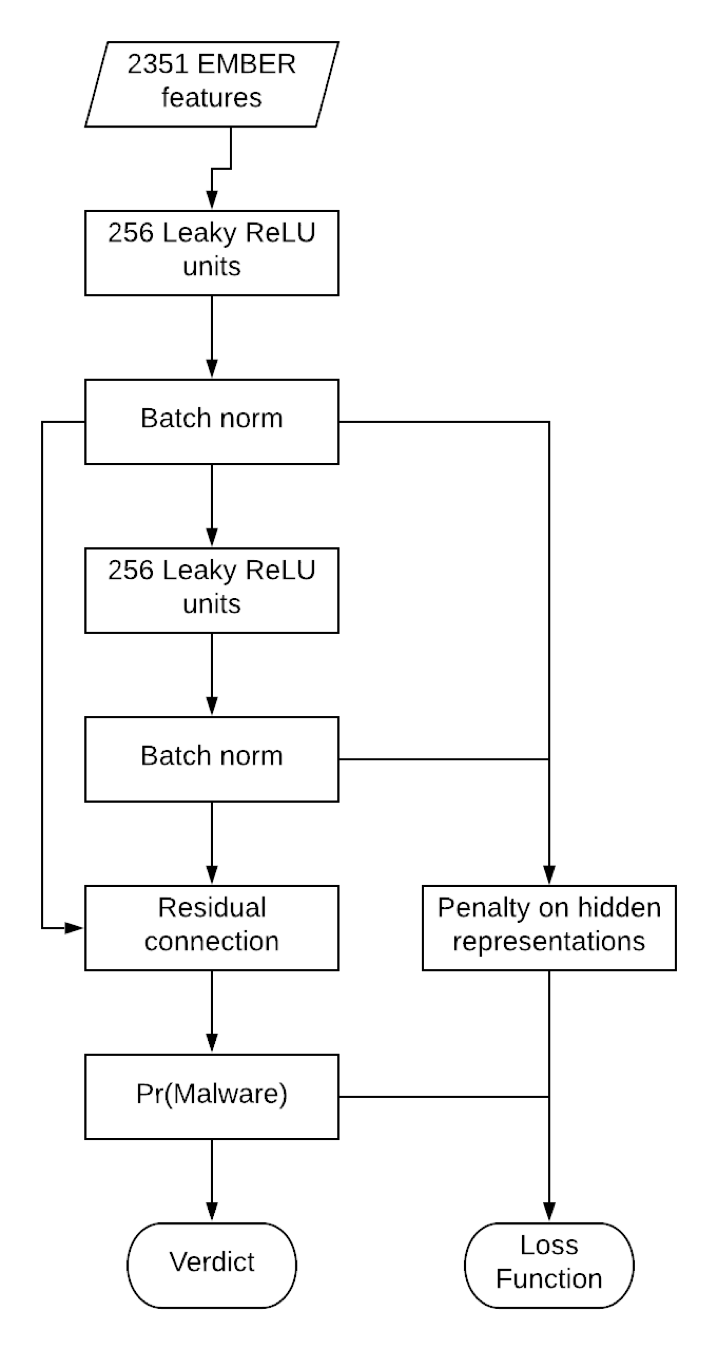 Figure 2. Diagram of how loss function and verdict are computed using novel regularization.
The network architecture in Figure 2 is a feedforward neural network with batch norm and a residual connection. We made no effort to optimize this network architecture. It’s probably true that a deeper or more elaborate network structure could be a better model; however, that’s beside the point.
Figure 2. Diagram of how loss function and verdict are computed using novel regularization.
The network architecture in Figure 2 is a feedforward neural network with batch norm and a residual connection. We made no effort to optimize this network architecture. It’s probably true that a deeper or more elaborate network structure could be a better model; however, that’s beside the point. Figure 3. The magnitude of the difference in the hidden representations tends to be smaller for the regularized model (blue), as shown by the darker smoothing line.
Second, we show that the novel regularization method improves the robustness of the model (when selecting the correct level of regularization
Figure 3. The magnitude of the difference in the hidden representations tends to be smaller for the regularized model (blue), as shown by the darker smoothing line.
Second, we show that the novel regularization method improves the robustness of the model (when selecting the correct level of regularization 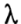 ). Figure 4 compares the regularized model with various levels of the novel penalty applied. It demonstrates that
). Figure 4 compares the regularized model with various levels of the novel penalty applied. It demonstrates that 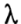 values on the order of 0.01 or 0.001 worked well, while using larger regularization diminishes the effectiveness of the model. The blue line and band show the effectiveness of the baseline model with no regularization applied, and the 95 percent confidence interval.
values on the order of 0.01 or 0.001 worked well, while using larger regularization diminishes the effectiveness of the model. The blue line and band show the effectiveness of the baseline model with no regularization applied, and the 95 percent confidence interval.
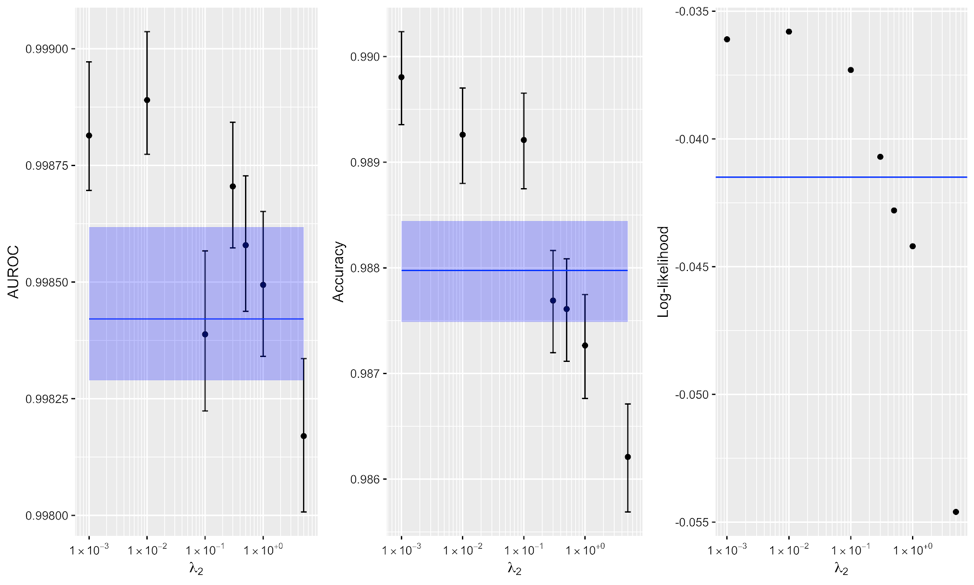 Figure 4. Comparison of baseline models (blue) to several alternative regularized models, for varying levels of regularization for three different metrics of model quality. Certain regularization penalties
Figure 4. Comparison of baseline models (blue) to several alternative regularized models, for varying levels of regularization for three different metrics of model quality. Certain regularization penalties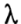 demonstrate that the regularized model has statistically significant improvement over the baseline model (CIs omitted for log-likelihood.)
The observation that too large a regularization penalty decreases model fit is consistent with the workings of other regularization methods, such as weight decay or dropout. All regularization seeks to trade an increase in statistical bias for a larger decrease in statistical variance, thereby reducing total error. If the regularization penalty is set too large, the increase in bias is so large that the model cannot fit the data appropriately, so the model quality is lower. Typically, there is a “sweet spot” of regularization magnitude where the model achieves a balance between overfitting and underfitting the data, and this is what we find in Figure 4.
Third, we test how hard it is to take a malware sample which is detected, then modify it to be non-detected. This is a different experiment because it is closer to how an adversary would approach the problem of evading a deployed malware classifier: If their malicious payload is detected, they can try to evade it again and again.
Figure 5 shows that the regularized model detects the modified samples at consistently higher rates than the baseline model (shown in blue), and that this difference is statistically significant for all regularized models.
demonstrate that the regularized model has statistically significant improvement over the baseline model (CIs omitted for log-likelihood.)
The observation that too large a regularization penalty decreases model fit is consistent with the workings of other regularization methods, such as weight decay or dropout. All regularization seeks to trade an increase in statistical bias for a larger decrease in statistical variance, thereby reducing total error. If the regularization penalty is set too large, the increase in bias is so large that the model cannot fit the data appropriately, so the model quality is lower. Typically, there is a “sweet spot” of regularization magnitude where the model achieves a balance between overfitting and underfitting the data, and this is what we find in Figure 4.
Third, we test how hard it is to take a malware sample which is detected, then modify it to be non-detected. This is a different experiment because it is closer to how an adversary would approach the problem of evading a deployed malware classifier: If their malicious payload is detected, they can try to evade it again and again.
Figure 5 shows that the regularized model detects the modified samples at consistently higher rates than the baseline model (shown in blue), and that this difference is statistically significant for all regularized models.
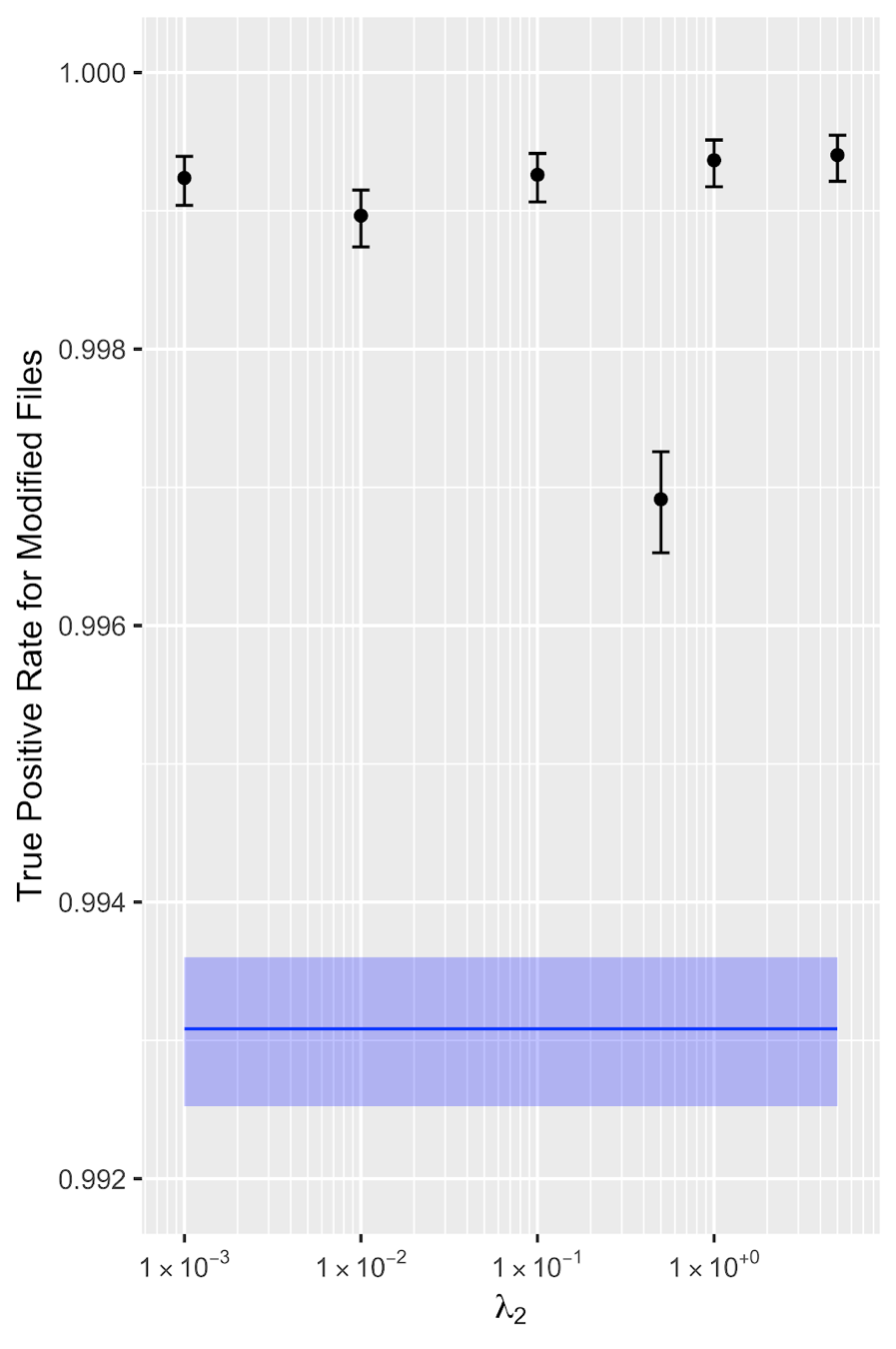 Figure 5. For all levels of regularization, the regularized model is consistently more difficult to evade using random ASCII text, compared to the baseline model (blue).
Taken together, these results provide some evidence that the regularized models are more robust to adversarial models compared to baseline models. We recommend that security researchers should leverage these and similar results when considering machine learning models for computer security.
Beyond ASCII Modifications
Additionally, we believe that this method will be robust to alternative strategies which add “chaff” data to the PE file. For example, additional modification strategies could include adding dummy sections that are never referenced, or import functions that are never called. This regularization method does not depend on the particular type of modification applied to a file. This is because the regularization only cares about the comparison of the hidden representations of the modified and non-modified files. For this reason, we believe that this same strategy can be adapted to other types of modifications.
We experimented with these types of augmentations but discovered a quirk with how the Ember feature space works. We applied some of these modifications using the open source executable-parsing library LIEF (library to instrument executable formats); however, we discovered that applying the modifications resulted in a PE file which LIEF, and by extension the Ember feature extractor which relies on LIEF, would then refuse to parse.
This blog outlines a simple method to improve the robustness of neural networks for static analysis. This method works by penalizing the norm of the difference in the hidden representations of a software sample and its modified “twin.” We have shown some evidence that this method is effective in the case of evasion which appends ASCII bytes to the overlay, and suspect that it may be effective against other modifications that append “chaff” data to a PE file.
David J. Elkind is a senior data scientist at CrowdStrike Inc., and holds an M.S. in mathematics from Georgetown University.
Figure 5. For all levels of regularization, the regularized model is consistently more difficult to evade using random ASCII text, compared to the baseline model (blue).
Taken together, these results provide some evidence that the regularized models are more robust to adversarial models compared to baseline models. We recommend that security researchers should leverage these and similar results when considering machine learning models for computer security.
Beyond ASCII Modifications
Additionally, we believe that this method will be robust to alternative strategies which add “chaff” data to the PE file. For example, additional modification strategies could include adding dummy sections that are never referenced, or import functions that are never called. This regularization method does not depend on the particular type of modification applied to a file. This is because the regularization only cares about the comparison of the hidden representations of the modified and non-modified files. For this reason, we believe that this same strategy can be adapted to other types of modifications.
We experimented with these types of augmentations but discovered a quirk with how the Ember feature space works. We applied some of these modifications using the open source executable-parsing library LIEF (library to instrument executable formats); however, we discovered that applying the modifications resulted in a PE file which LIEF, and by extension the Ember feature extractor which relies on LIEF, would then refuse to parse.
This blog outlines a simple method to improve the robustness of neural networks for static analysis. This method works by penalizing the norm of the difference in the hidden representations of a software sample and its modified “twin.” We have shown some evidence that this method is effective in the case of evasion which appends ASCII bytes to the overlay, and suspect that it may be effective against other modifications that append “chaff” data to a PE file.
David J. Elkind is a senior data scientist at CrowdStrike Inc., and holds an M.S. in mathematics from Georgetown University.
 Join CrowdStrike: If you’re ready to work on unrivaled technology that's processing data at unprecedented scale, please check out our
Join CrowdStrike: If you’re ready to work on unrivaled technology that's processing data at unprecedented scale, please check out our
Effective practitioners should be wary of these weaknesses and take steps to harden their models against them. In this blog, I outline a specific variety of adversarial attack in the static analysis setting: appending text to the overlay of a PE (portable executable) file. I also demonstrate a novel regularization method that can harden neural network models against that attack. This regularization method is generically applicable against similar attacks that append “chaff” data to a PE file. The following offers an overview of research I’ve been conducting and will be presenting at the Conference on Applied Machine Learning for Information Security (CAMLIS) in Washington, D.C., on Oct. 25-26, 2019. CrowdStrike® scientists are pursuing novel research in the area of computer security and machine learning because we are aware of certain shortcomings in some machine learning models. This is why we are investing resources to improve these models and harden them against attack.
Simple Tactics for Evading Machine Learning in Computer Security
In some cases, simple modifications to PE files can cause machine learning models to misclassify the file. For example, at DEFCON 2019, William Fleshman won the Machine Learning Static Evasion Competition with a 100 percent evasion rate using ASCII data appended or inserted into PE files. The security implications are obvious: If the difference between detecting and not detecting malware is a matter of a few errant strings, then the machine learning isn’t doing its job.Even though appending ASCII text to a PE file does not change its operation, it can change its feature vector. A feature vector is a summary of what a PE file “looks like,” and it works by measuring file information that researchers believe is relevant to the file’s maliciousness. In this project, we use the open-source Ember feature vectors. (See Anderson & Roth, “EMBER: An Open Dataset for Training Static PE Malware Machine Learning Models” for a detailed discussion.) The Ember data set and feature vectors are completely different from CrowdStrike’s data and feature vectors. In particular, the Ember feature vector measures the file size, the size of the overlay and the entropy of the entire file, as well as constructing an entropy histogram of the file. To the extent that a machine learning model uses these particular features in its classification decision, so too will the machine learning model be sensitive to deliberate attempts to mislead the model and give erroneous decisions by modifying these feature values. We find that our regularization strategy is able to make a neural network model more robust to this evasion strategy.
 Figure 1 is a toy example of the classification boundary of a machine learning model using two input features x1, x2 . Some of the malicious examples fall on the wrong side of the boundary, so they are evasive. Additionally, some of the benign examples are false-positives because they are misclassified as malicious.
Figure 1 is a toy example of the classification boundary of a machine learning model using two input features x1, x2 . Some of the malicious examples fall on the wrong side of the boundary, so they are evasive. Additionally, some of the benign examples are false-positives because they are misclassified as malicious.
A Novel Strategy for Robustness
A secure machine learning model should not be confused by modifications that leave malicious functionality intact, such as the addition of ASCII strings. Instead, the ideal model would have the same representation for the original and the modified files.This observation is the motivation for my proposed method of hardening machine learning models. In my regularization method, the model is trained with an additional regularization term, which penalizes discrepancy between some samples and the same samples with appended text.
In particular, training proceeds in the following fashion:
- For each sample in the corpus, create a “twin” sample which appends random ASCII text to the overlay.
- Extract feature vectors for both the original and the “twin” sample.
- Add a regularization term to the model to penalize differences in the hidden representations for each pair of samples:
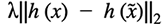
. This penalty exactly matches the original description of the problem in the sense that this penalty is minimized at 0 when the two representations are the same. In other words, the penalty encourages the model to have the same hidden representation for the modified and unmodified files. The tuning parameter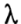
governs how much of a penalty to assign to the difference in representations. In our experiments, we found that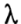 values on the order of 0.01 or 0.001 worked well.
values on the order of 0.01 or 0.001 worked well.
 Figure 2. Diagram of how loss function and verdict are computed using novel regularization.
The network architecture in Figure 2 is a feedforward neural network with batch norm and a residual connection. We made no effort to optimize this network architecture. It’s probably true that a deeper or more elaborate network structure could be a better model; however, that’s beside the point.
Figure 2. Diagram of how loss function and verdict are computed using novel regularization.
The network architecture in Figure 2 is a feedforward neural network with batch norm and a residual connection. We made no effort to optimize this network architecture. It’s probably true that a deeper or more elaborate network structure could be a better model; however, that’s beside the point.The purpose of this research is to show that the regularized model can beat the baseline model. We believe this regularization strategy will improve robustness across alternative network specifications, because it changes how neural networks interpret pairs of modified and non-modified samples. When considering how this regularization works, we believe that it is effective because it encourages the model to give less weight to the particular features that are manipulated by appending ASCII data, or at least to ignore the changes which arise from appending random ASCII bytes to the end of the file.
Otherwise, training proceeds in the ordinary way. In these experiments, we used cross-entropy loss and the Adam optimizer with a fixed learning rate and mini-batches of 128 pairs of feature vectors. Probability estimates are computed using the softmax activation in the final layer. We used the PE files and feature vectors from the Ember 2017 dataset. This method is simple to implement in any modern neural network library; you just have to return the hidden state along with the model predictions, and add a term to the loss function.
Experimental Results
Our experiments confirm that this simple method is effective at improving the robustness of machine learning models to evasion attempts that append ASCII text to PE files. We conducted several experiments to evaluate the effectiveness of this regularization method and the results are encouraging. When reviewing these results, it’s important to keep in mind that this analysis was conducted using the open-source Ember data set and feature vectors. These are completely different from the data sources and proprietary feature extraction engines that CrowdStrike uses in its products. Therefore, these results do not have any bearing on the efficacy of any of CrowdStrike’s machine learning models, because training a model on different data gives a different result. First, we demonstrate that the regularization method is working as intended. Figure 3 shows the discrepancy between modified and non-modified pairs of files as training progresses. The regularized model is shown in blue, and the baseline model is shown in red. The vertical axis shows the magnitude of the norm of the difference, and the horizontal axis shows the number of pairs seen by the model. After the initial stage of training, the darker smoothing line shows that the norm of the difference between modified and non-modified pairs is consistently smaller, implying that the model is encouraged to think of both files as similar. Figure 3. The magnitude of the difference in the hidden representations tends to be smaller for the regularized model (blue), as shown by the darker smoothing line.
Second, we show that the novel regularization method improves the robustness of the model (when selecting the correct level of regularization
Figure 3. The magnitude of the difference in the hidden representations tends to be smaller for the regularized model (blue), as shown by the darker smoothing line.
Second, we show that the novel regularization method improves the robustness of the model (when selecting the correct level of regularization  Figure 4. Comparison of baseline models (blue) to several alternative regularized models, for varying levels of regularization for three different metrics of model quality. Certain regularization penalties
Figure 4. Comparison of baseline models (blue) to several alternative regularized models, for varying levels of regularization for three different metrics of model quality. Certain regularization penalties Figure 5. For all levels of regularization, the regularized model is consistently more difficult to evade using random ASCII text, compared to the baseline model (blue).
Taken together, these results provide some evidence that the regularized models are more robust to adversarial models compared to baseline models. We recommend that security researchers should leverage these and similar results when considering machine learning models for computer security.
Beyond ASCII Modifications
Additionally, we believe that this method will be robust to alternative strategies which add “chaff” data to the PE file. For example, additional modification strategies could include adding dummy sections that are never referenced, or import functions that are never called. This regularization method does not depend on the particular type of modification applied to a file. This is because the regularization only cares about the comparison of the hidden representations of the modified and non-modified files. For this reason, we believe that this same strategy can be adapted to other types of modifications.
We experimented with these types of augmentations but discovered a quirk with how the Ember feature space works. We applied some of these modifications using the open source executable-parsing library LIEF (library to instrument executable formats); however, we discovered that applying the modifications resulted in a PE file which LIEF, and by extension the Ember feature extractor which relies on LIEF, would then refuse to parse.
This blog outlines a simple method to improve the robustness of neural networks for static analysis. This method works by penalizing the norm of the difference in the hidden representations of a software sample and its modified “twin.” We have shown some evidence that this method is effective in the case of evasion which appends ASCII bytes to the overlay, and suspect that it may be effective against other modifications that append “chaff” data to a PE file.
David J. Elkind is a senior data scientist at CrowdStrike Inc., and holds an M.S. in mathematics from Georgetown University.
Figure 5. For all levels of regularization, the regularized model is consistently more difficult to evade using random ASCII text, compared to the baseline model (blue).
Taken together, these results provide some evidence that the regularized models are more robust to adversarial models compared to baseline models. We recommend that security researchers should leverage these and similar results when considering machine learning models for computer security.
Beyond ASCII Modifications
Additionally, we believe that this method will be robust to alternative strategies which add “chaff” data to the PE file. For example, additional modification strategies could include adding dummy sections that are never referenced, or import functions that are never called. This regularization method does not depend on the particular type of modification applied to a file. This is because the regularization only cares about the comparison of the hidden representations of the modified and non-modified files. For this reason, we believe that this same strategy can be adapted to other types of modifications.
We experimented with these types of augmentations but discovered a quirk with how the Ember feature space works. We applied some of these modifications using the open source executable-parsing library LIEF (library to instrument executable formats); however, we discovered that applying the modifications resulted in a PE file which LIEF, and by extension the Ember feature extractor which relies on LIEF, would then refuse to parse.
This blog outlines a simple method to improve the robustness of neural networks for static analysis. This method works by penalizing the norm of the difference in the hidden representations of a software sample and its modified “twin.” We have shown some evidence that this method is effective in the case of evasion which appends ASCII bytes to the overlay, and suspect that it may be effective against other modifications that append “chaff” data to a PE file.
David J. Elkind is a senior data scientist at CrowdStrike Inc., and holds an M.S. in mathematics from Georgetown University.
open engineering and technology positions.
Additional Resources
- Download a white paper to learn more: “The Rise of Machine Learning in Cybersecurity.”
- Learn more about the CrowdStrike Falcon®® platform by visiting the product page.
- Test CrowdStrike next-gen AV for yourself. Start your free trial of Falcon Prevent™ today.




![Helping Non-Security Stakeholders Understand ATT&CK in 10 Minutes or Less [VIDEO]](https://assets.crowdstrike.com/is/image/crowdstrikeinc/video-ATTCK2-1)
![Qatar’s Commercial Bank Chooses CrowdStrike Falcon®: A Partnership Based on Trust [VIDEO]](https://assets.crowdstrike.com/is/image/crowdstrikeinc/Edward-Gonam-Qatar-Blog2-1)













































