Re-searching Hyperparameters for Training Boosted Tree Models

Introduction
While deep neural networks have state-of-the-art performance in many tasks, boosted tree models still often outperform deep neural networks on tabular data. This largely seems to be the case because tabular data has natural boundaries perpendicular to input dimensions, and boosted tree models already naturally create such boundaries, while neural networks have to learn to create boundaries perpendicular to feature axes.
In constructing a boosted tree model, various hyperparameters control how the trees are created. Some control the depth of trees or whether splits are created, while others control things like the magnitude of the values of the leaves used in creating a prediction value. Some search over the hyperparameters is necessary to produce a highly optimized model, so we will outline one method of doing this hyperparameter search.
Background
Because boosted tree models are built in rounds (usually one tree at a time), any hyperparameters of the model that affect how trees are built (which is most of them) can be changed between rounds. For instance, the learning rate might be varied from higher in the beginning of training to lower later in training.
There are many ways of adjusting hyperparameters during training, such as Population-Based Training [1], but we will describe a very simple way of accomplishing this using repeated application of the Successive Halving algorithm [2]. In the Successive Halving algorithm, some number of models are initialized with hyperparameters chosen randomly. The models are run for some amount of time (in this case, either boosting rounds or actual wall clock time) and the best half are chosen to continue running longer. This process repeats until a single model is chosen. After a single model is chosen, we run this model until early stopping (the model hasn’t improved its validation loss in some number of boosting rounds).
After running Successive Halving, we know that we have a final model that performs well, but we also know, because the early stopping condition was met, that we can’t get much more out of continuing to train that model with the set of hyperparameters that were used to train it. So we need to try other hyperparameters if we want to continue training that model.
Repeated Successive Halving
After we’ve run through the Successive Halving algorithm once, and we have a model that has reached early stopping, we can use the best model so far to initialize another set of models with randomly chosen hyperparameters, run Successive Halving again, and we can do this repeatedly.
Repeated Successive Halving allows us to use different sets of hyperparameters earlier and later in training and to get the last little bit of performance out of our models. It’s also a simple procedure that is easy to implement.
There are some things about this to keep in mind though. Because the validation loss is used repeatedly and used to judge many different models, it is important that the validation set be large enough and representative enough of the true data distribution to be used in this way. If the validation set is too small or does not represent the true data distribution well enough, then this procedure can overfit to the validation set.
Results
As we see in Figure 1, most of the improvement in validation loss is found by the best model in the first round of Successive Halving, but the early stopping criteria stops that model from training. Then, after running Successive Halving again, we get a slightly better loss.
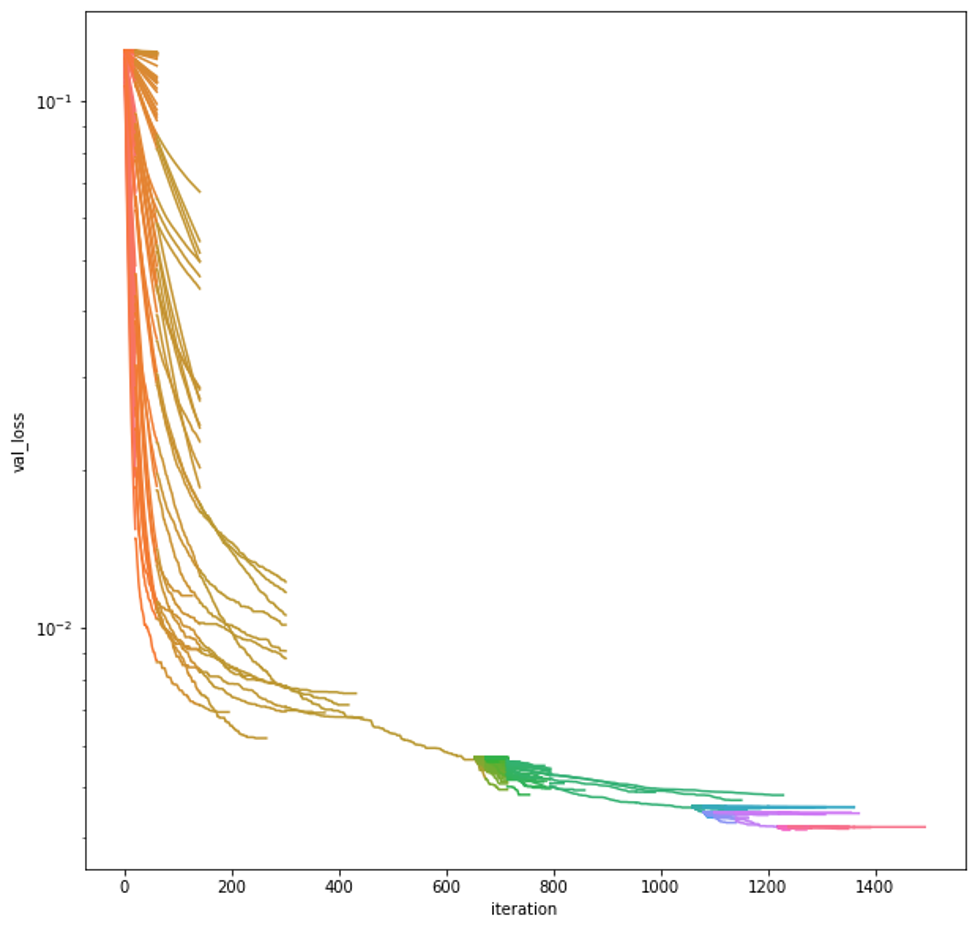
Figure 1. Validation loss through XGBoost boosting iterations of models during hyperparameter search. Each line is a different model, with the color indicating the first model created (orange-red) to the last model created (hot pink).
In Table 1, we have some hyperparameters that were chosen as the best in each round. After five rounds, we have a model with almost twice as many trees as the first early-stopped model has. The learning rate bounces around a bit between rounds, but the later rounds with higher learning rates (rounds 3 and 5) were not able to add many trees to the model because they were early-stopped. This effectively gives a learning rate that is high early in training, but low later in training, because most of the trees added later in training were added with a lower learning rate. Another interesting result is that the chosen L1 or L2 regularization is moderate for at least one of L1 or L2, but never very low for both.
| Successive Halving Round | Total Iterations Until Early Stopping | Learning Rate | Min. Child Weight | L2 Regularization | L1 Regularization | Colsample by Tree | Instance Subsample |
| Round 1 | 654 | 0.083 | 0.0072 | 0.39 | 4.7e-08 | 0.29 | 0.70 |
| Round 2 | 1060 | 0.011 | 5.7e-06 | 0.026 | 4.1e-10 | 0.76 | 0.92 |
| Round 3 | 1080 | 0.080 | 0.0084 | 1.8e-07 | 0.063 | 0.71 | 0.63 |
| Round 4 | 1220 | 0.0032 | 2.6e-09 | 0.17 | 1.0e-09 | 0.27 | 0.59 |
| Round 5 | 1261 | 0.059 | 0.00040 | 3.5e-07 | 0.0036 | 0.5 | 0.5 |
Table 1. Chosen XGBoost hyperparameters for the best model in each round of Successive Halving when optimizing on a toy dataset.
Keep in mind that the best final model at the end of this procedure has been trained with all of the hyperparameters in Table 1 in succession.
Conclusion
We have described a simple procedure for training a boosted tree model with hyperparameters that change during training to get a more optimal model than one trained with only a single set of hyperparameters. This procedure can be especially useful for difficult datasets with complex decision boundaries that can benefit from the extra layer of optimization that this procedure provides.
References
[1] Jaderberg, Max, Valentin Dalibard, Simon Osindero, Wojciech M. Czarnecki, Jeff Donahue, Ali Razavi, Oriol Vinyals et al. “Population based training of neural networks.” arXiv preprint arXiv:1711.09846 (2017).
[2] Jamieson, Kevin, and Ameet Talwalkar. “Non-stochastic best arm identification and hyperparameter optimization.” In Artificial Intelligence and Statistics, pp. 240-248. PMLR, 2016.

